Introduction
Loss functions tell the algorithm how far we are from actual truth, and their gradients/derivates help understand how to reduce the overall loss (by changing the parameters being trained on)
All losses in keras defined here
But why is the loss function expressed as a negative loss?
Plot: 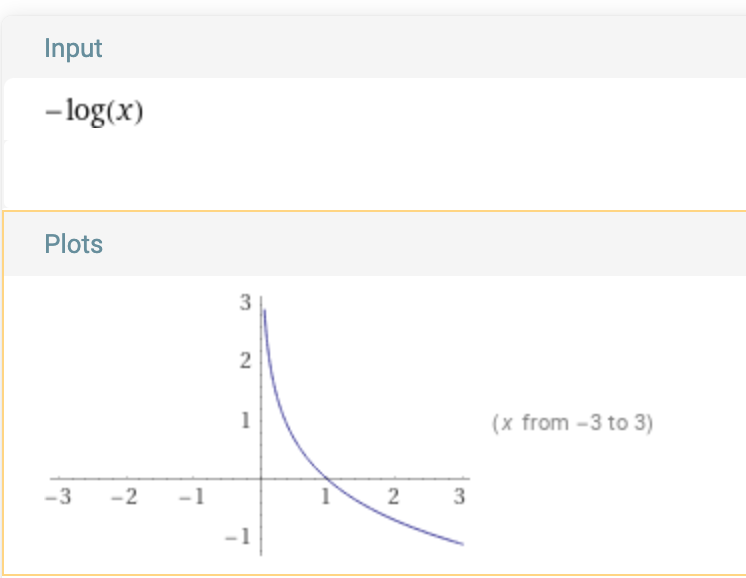
As probabilities only lie between [0-1], the plot is only relevant between X from 0-1
This means, that it penalises a low probability of success exponentially more.
But since we do LogLoss = - ( y * Log(p(y)) )
If the true label is 0, the effect of the log is ignored.
Only true labels contribute to the overall loss, and if for the true labels the P(y) value is low, then the loss magnitude is highly penalised
What are logits?
In context of deep learning the logits layer means the layer that feeds in to softmax (or other such normalization).
The output of the softmax are the probabilities for the classification task and its input is logits layer.
The logits layer typically produces values from -infinity to +infinity and the softmax layer transforms it to values from 0 to 1.
Why do we make the loss functions take the logit values instead of the final classification labels?
Pushing the “softmax” activation into the cross-entropy loss layer significantly simplifies the loss computation and makes it more numerically stable.
Full derivation in this SO post
Binary Cross Entropy
Math:
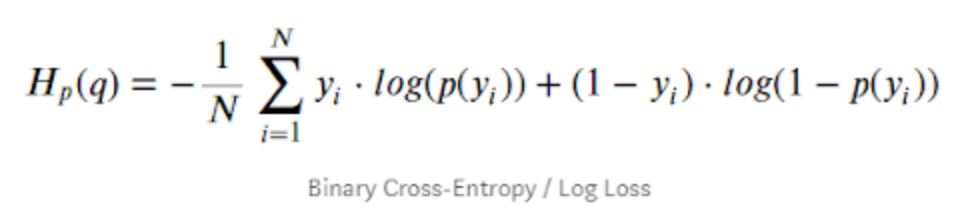
This is just expanded math for using P(0) = { 1 - P(1) }, and becomes same as log loss
The hypthosis/P function used is typically sigmoid
Used for:
When the output class is one of two values (binary) in nature.
Code:
# Compute cross entropy from probabilities.
bce = target * tf.math.log(output + epsilon())
bce += (1 - target) * tf.math.log(1 - output + epsilon())
Categorical cross entropy
Math:
Used for:
If your 𝑌 vector values are one-hot encoded, use categorical_crossentropy.
Examples (for a 3-class classification): [1,0,0] , [0,1,0], [0,0,1]
Sparse Categorical Cross Entropy
Math (same as Categorical Cross Entropy)
Used for:
Integer classes as output
Intuitively, the sparse categorical just takes the index of the true-value to calculate the loss
So when model output is for example [0.1, 0.3, 0.7] and ground truth is 3 (if indexed from 1) then loss compute only logarithm of 0.7. This doesn’t change the final value, because in the regular version of categorical crossentropy other values are immediately multiplied by zero (because of one-hot encoding characteristic). Thanks to that it computes logarithm once per instance and omits the summation which leads to better performance.
